Readings in Database Systems - Interactive Analytics
最近在看 Stonebraker 的 “Readings in Database Systems”, 发觉开拓了很多思路。
这么多年自己一直在从事大数据方面的工作,但除了翻过数据挖掘算法和分布式系统设计方面的论文外,完全没想过去翻翻数据库相关的论文看。现在想想,其实大数据和数据库两者很多需求和场景是一致的,要解决的问题,没准学术界很多年前就已经有方案了。
这篇文章主要是 "Interactive Analytics" 相关部分。
What is Interactive Analytics
假如你是一家电商公司的分析师,如果有 100 万用户原始交易数据打印出来摆在你面前,让你去分析这些数据的意义,你会怎么做?
如果这十万条数据给我,我估计是看不出什么东西出来。而且我相信每个人,也是如此,因为人的认知是有 bug 的,比如不能直接处理大量原始数据。
那该怎么办?
我们需要把数据通过一些方式做提炼,变成小的结果集,或者以可视化的形式展现出来。用过
SQL 的人也许会想到 Group by
语句,是的,往往通过 Group by 做 aggregation
后的数据,会好理解很多。
大数据不只是数据量超大,更在于能从大量数据里面发现价值。
而 "Interactive Analytics" 指的就是这个过程,但加了个前提:这个过程必须能在较短的时间内完成,哪怕甚至来不及遍历所有需要的原始数据。
当数据量超大的时候,这个前提对每个数据系统都是一个很大的挑战。
Ideas
那怎么让一个查询请求的执行过程比直接遍历所有依赖的数据还快呢?
结论,显而易见,只能不去遍历所有的依赖数据,能有这样的方案,那问题也就迎刃而解了。
目前靠谱的方案有两种:
Precomputing,如果预先把查询请求依赖的相关数据都做了一定的 “提炼”,便可大大减少查询需要去遍历的数据。Sampling,可以对数据进行取样,每次查询请求都只遍历取样后的数据,这样遍历数据也可以大大减少。
“Red Book” 给出了四篇参考文献,1,2是关于 Precomputing 的,3,4是关于 Sampling
的。
Precomputing
Data Cube
还是以之前的交易数据举例,假如我们只关注零部件(Part)、供应商(Supplier)和客户(Customer)三个维度,关注的指标是总销售额,那么我们预先可以分别把每个不同部件
p、供应商 s、客户 c 的销售额总和统计出来,以 (p, s, c)
形式存起来,如果有相关查询请求,直接返回结果就可以了。
这就是一个三维 Data Cube 的建立和使用,每一个 cell
代表一种部件、供应商、客户组合 (p, s, c),对应的 value
就是这个组合的销售额总计。
Build Data Cube
当然,实际情况下,分析任务关注的维度肯定不仅是三个,可能是多个不同的维度组合。
对 data cube 的建立有如下三种方式:
- 预先计算出所有组合的 data cube,之后所有的请求就可以得到最快的响应,但会带来很大的预计算和数据存储压力。(如果有 K 的维度,需要执行 \[2^k\] 个 Group by 语句来做预计算。)
- 不做任何预计算,每个请求都直接从原始数据进行提取,这种方式没有额外的数据存储压力,但数据量大的情况下请求执行耗时会非常长。
- 预先计算一些维度组合的 data cube,这个是 1 采取的方式,这种方式目标是做到请求执行耗时、预计算耗时和存储的平衡,但选择哪些维度组合做预计算是关键,选择错了,可能还不如采用上面两种方式。
前面的例子,要全部预计算出部件、供应商和客户三个维度的 data cube,需要如下 8 个组合:
- psc (part, supplier, customer) (6M: 6 million rows)
- pc (part, customer) (6M)
- ps (part, supplier) (0.8M)
- sc (supplier, customer) (6M)
- p (part) (0.2M)
- s (supplier) (0.01M)
- c (customer) (0.1M)
- none (1)
(组合后面的数字代表该组合所有结果数据的行数)
可以发现,其实如果 psc 的数据有了,pc
可以通过按 supplier 维度汇聚 psc
的数据得到,p 可以通过按 cutomer 维度汇聚
pc 的数据得到,其他依次类推。
pc 组合和 psc 组合都有 6
百万行记录,也就是对 pc 和 psc
两个维度组合进行查询都要遍历这么多行记录,那么如果不预计算
pc,而在用户请求 pc 维度时直接通过对
psc
维度进行汇聚,遍历的数据行数是一致的,如果以数据行数作为衡量指标,预计算
pc 便是毫无必要的。
The Lattice Framework
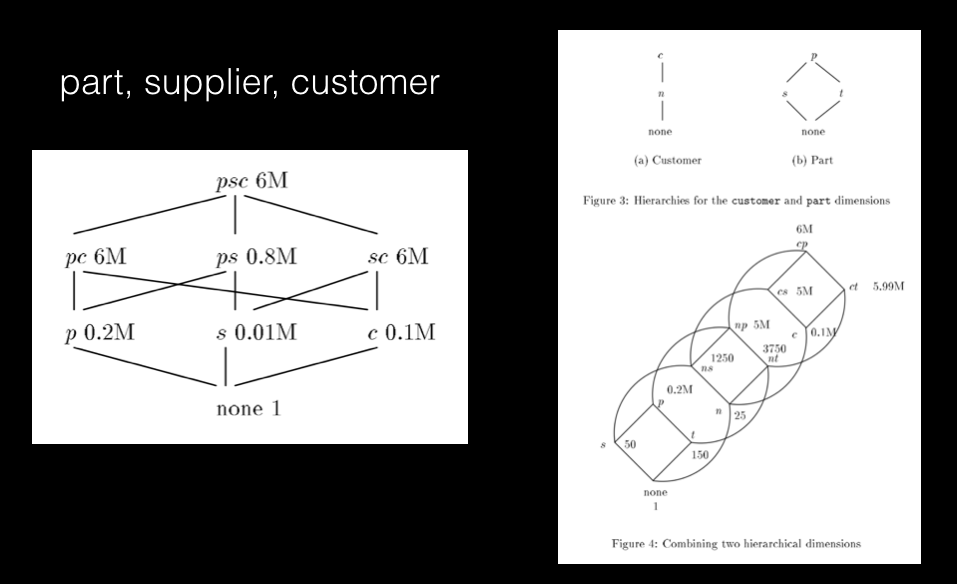
1 中提出了一个 Lattice 模型,如下图所示:
每个节点表示一个 data cube 组合,下方的节点可以通过上方节点汇聚得到。
左边是上面例子的 lattice 模型,右边是模型之间的合并过程。
通过这样的结构,可以将维度组合选择转化为一个最优选择的问题:
在限制节点个数的情况下,最小化每个节点预计算的平均耗时。
1 中首先提出了个 cost model 来评估通过依赖节点计算自身 data cube 的 cost,然后提出了个 greedy algorithm 通过计算平均最少 cost 来进行预计算维度选择,算法的细节和证明大家可以细读该论文。
2 中给出了一种基于内存的 data cube 计算方法,有兴趣可以下载阅读。
Sampling
Data Cube 模式,不论如何优化,都是需要离线任务去预先构建大量的 Cube 集,在需要的维度很多、或者数据延迟要求很低的场景下,不能很好的满足要求。
Sampling 方式是在降低准确性的前提下,减少遍历的数据量,达到快速响应查询请求的目的。
4 中通过对用户的查询请求进行统计,评估出经常用的查询列集合,预先进行 Sample 创建。
Sample Creation
如何进行 Sample 创建,我在看论文的时候,直接想到的是将数据记录打乱,随机分布在若干个 partition 里面,当有请求过来的时候,直接选择一个或多个 partition 进行查询即可。
4 中提到了这样做(uniform sampling)的问题:
如果只是全局的对数据做统计,效果比较好,但如果有 filter 或者 group by 操作,这种方式往往得不到好的效果。
举个例子,比如我要按城市来统计销售额的分布,如果是采用我想的那种分布方式的话,一些交易量很少的城市,可能在 sample 里完全消失了,这样的分布统计,其实是错的。
4 中提出了 Stratified Sampling 方式来解决这个问题。
基本思想就是首先对维度列进行统计,将相同列值的行作为一个 group,然后分别进行 sampling,论文中详细介绍了 sampling 的方法和每个 group sampling size 的设定。
Sample Selection
在如何选择 Sample 的问题上,4 提出了 ELP(Error Latency Profile)模型,通过用户设定的准确率和耗时要求,进行 sample 选择。
当然,这是个非常复杂的过程。4 中详细讲了如何去评估各个 Sample 的耗时和准确率,怎么样在生成执行计划的过程中考虑用户的准确率和耗时的要求。有兴趣大家可以详细阅读。
3 通过提出的如随机数据访问、在线排序、ripple join 等算法,在已有的关系型数据库,实现了一套支持 online sampling 的原型系统,有兴趣可以详细阅读。
Summary
Data Cube 方案,在数据的准确度方面是毋须质疑优于 Sampling 方案的,工程界的 Apache Kylin 就是如此的方式。而 Sampling 方式目前的应用还比较少,对于很多用户而言,Sampling 的方案即使是 99% 的准确度,还是无法接受的,哪怕其实已经满足了他的需求。
但我倒比较看好 Sampling 方式,因为 Data Cube 的整个机制对数据变化和实时方面有很大的限制,随着内存越来越廉价,以及越来越好的列存储方案,数据进行实时交互分析变得越来越可行,比如 Impala 和 Presto,在大数据量的情况下,性能都很好,不大的集群都可以做到秒级响应对亿级数据量的查询。
当然,资源不可能是无限的,也不可能每个查询请求都能有资源保证快速遍历海量数据,所以,通过对准确率方面的牺牲,达到查询耗时的降低,其实是一种比较经济的方案 (Presto 是有类似 4 中提到的 Sampling 方案)。
Reference